ch.ethz.idsc.owl

Library for motion planning in Java, version 0.5.9

The library was developed with the following objectives in mind

• suitable for use in safety-critical real-time systems
• trajectory planning for an autonomous vehicle
• implementation of theoretical concepts with high level of abstraction
• simulation and visualization

Student Projects

2017

• Jonas Londschien (MT): An Anytime Generalized Label Correcting Method for Motion Planning

2018

• Yannik Nager (MT): What lies in the shadows? Safe and computation-aware motion planning for autonomous vehicles using intent-aware dynamic shadow regions

2019

• André Stoll (MT): Multi-Objective Optimization Using Preference Structures
• Oliver Brinkmann (MT): Averaging on Lie Groups: Applications of Geodesic Averages and Biinvariant Means
• Joel Gächter (MT): Subdivision-Based Clothoids in Autonomous Driving

Features

• Motion planning algorithms: GLC, and RRT*
• integrators: Euler, Midpoint, Runge-Kutta 4-5th order, exact integrator for the group SE2
• state-space models: car-like, two-wheel-drive, pendulum-swing-up, Lotka-Volterra, etc.
• efficient heuristic for goal regions: sphere, conic section
• visualizations and animations, see video

Motion Planning

GLC

Rice2: 4-dimensional state space + time

SE2: 3-dimensional state space

Simulation: autonomous gokart or car

RRT*

R^2

Nearest Neighbors

Integration

Specify repository and dependency of the owl library in the pom.xml file of your maven project:

<repositories>
  <repository>
    <id>owl-mvn-repo</id>
    <url>https://raw.github.com/idsc-frazzoli/owl/mvn-repo/</url>
    <snapshots>
      <enabled>true</enabled>
      <updatePolicy>always</updatePolicy>
    </snapshots>
  </repository>
</repositories>

<dependencies>
  <dependency>
    <groupId>ch.ethz.idsc</groupId>
    <artifactId>owl</artifactId>
    <version>0.5.9</version>
  </dependency>
</dependencies>

Contributors

Jan Hakenberg, Jonas Londschien, Yannik Nager, André Stoll, Joel Gaechter

The code in the repository operates a heavy and fast robot that may endanger living creatures. We follow best practices and coding standards to protect from avoidable errors.

Publications

• What lies in the shadows? Safe and computation-aware motion planning for autonomous vehicles using intent-aware dynamic shadow regions by Yannik Nager, Andrea Censi, and Emilio Frazzoli, video

References

• A Generalized Label Correcting Method for Optimal Kinodynamic Motion Planning by Brian Paden and Emilio Frazzoli, arXiv:1607.06966, video
• Sampling-based algorithms for optimal motion planning by Sertac Karaman and Emilio Frazzoli, IJRR11

ch.ethz.idsc.sophus

Library for non-linear geometry computation in Java

The library was developed with the following objectives in mind

• trajectory design for autonomous robots
• suitable for use in safety-critical real-time systems
• implementation of theoretical concepts with high level of abstraction

Features

• geodesics in Lie-groups and homogeneous spaces: Euclidean space R^n, special Euclidean group SE(2), hyperbolic half-plane H2, n-dimensional sphere S^n, ...
• parametric curves defined by control points in non-linear spaces: GeodesicBSplineFunction, ...
• non-linear smoothing of noisy localization data GeodesicCenterFilter
• Dubins path

Geodesic DeBoor Algorithm

B-Spline curves in SE(2) produced by DeBoor Algorithm or curve subdivision produce curves in the planar subspace R^2 with appealing curvature.

Smoothing using Geodesic Averages

The sequence of localization estimates of a mobile robot often contains noise. Instead of using a complicated extended Kalman filter, geodesic averages based on conventional window functions denoise the uniformly sampled signal of poses in SE(2).

Curve Decimation in Lie Groups

The pose of mobile robots is typically recorded at high frequencies. The trajectory can be faithfully reconstructed from a fraction of the samples.

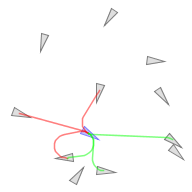
Visualization of Geodesic Averages

A geodesic average is the generalization of an affine combination from the Euclidean space to a non-linear space. A geodesic average consists of a nested binary averages. Generally, an affine combination does not have a unique expression as a geodesic average. Instead, several geodesic averages reduce to the same affine combination when applied in Euclidean space.

Contributors

Jan Hakenberg, Oliver Brinkmann, Joel Gächter

Publications

• Curve Subdivision in SE(2) by Jan Hakenberg, viXra:1807.0463, video
• Smoothing using Geodesic Averages by Jan Hakenberg, viXra:1810.0283, video
• Curve Decimation in SE(2) and SE(3) by Jan Hakenberg, viXra:1909.0174

References

• Bi-invariant Means in Lie Groups. Application to Left-invariant Polyaffine Transformations. by Vincent Arsigny, Xavier Pennec, Nicholas Ayache
• Exponential Barycenters of the Canonical Cartan Connection and Invariant Means on Lie Groups by Xavier Pennec, Vincent Arsigny
• Lie Groups for 2D and 3D Transformations by Ethan Eade
• Manifold-valued subdivision schemes based on geodesic inductive averaging by Nira Dyn, Nir Sharon
• Power Coordinates: A Geometric Construction of Barycentric Coordinates on Convex Polytopes by Max Budninskiy, Beibei Liu, Yiying Tong, Mathieu Desbrun