[Table of Contents]

• JuliaCall for Seamless Integration of R and Julia
  • Installation
  • Basic Usage
  • Troubleshooting and Ways to Get Help
  • JuliaCall for R Package Developers
  • Suggestion, Issue Reporting, and Contributing
  • Other Interfaces Between R and Julia

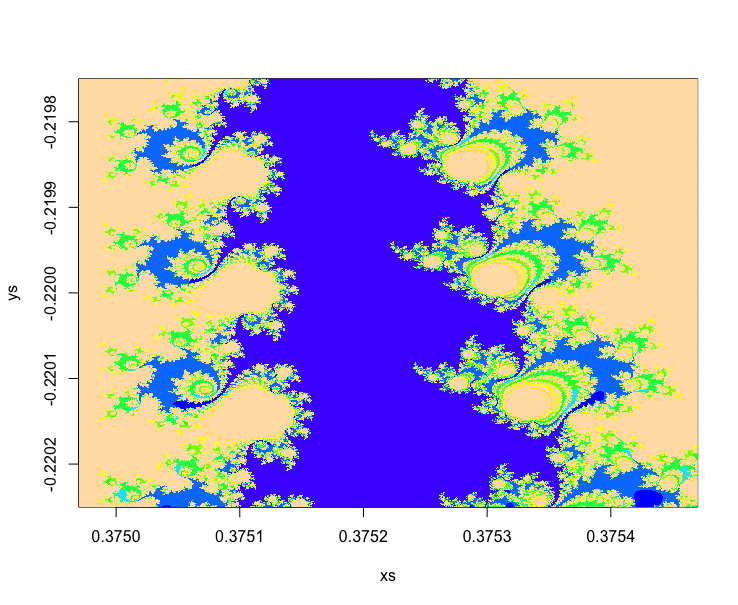
Package JuliaCall is an R interface to Julia, which is a high-level, high-performance dynamic programming language for numerical computing, see https://julialang.org/ for more information. Below is an image for Mandelbrot set. JuliaCall brings more than 100 times speedup of the calculation! See https://github.com/Non-Contradiction/JuliaCall/tree/master/example/mandelbrot for more information.

You can install JuliaCall just like any other R packages by

install.packages("JuliaCall")

To use JuliaCall you must have a working installation of Julia. This can be easily done via:

library(JuliaCall)
install_julia()

which will automatically install and setup a version of Julia specifically for use with JuliaCall. Or you can do

library(JuliaCall)
julia_setup(installJulia = TRUE)

which will invoke install_julia automatically if Julia is not found and also do initialization of JuliaCall.

You can also setup Julia manually by downloading a generic binary from https://julialang.org/downloads/ and add it to your path. Currently Julia v0.6.x and the Julia v1.x releases are all supported by JuliaCall.

You can get the development version of JuliaCall by

devtools::install_github("Non-Contradiction/JuliaCall")

Before using JuliaCall, you need to do initial setup by function julia_setup() for automatic type conversion, Julia display systems, etc. It is necessary for every new R session to use the package. If not carried out manually, it will be invoked automatically before other julia_xxx functions. Solutions to some common error in julia_setup() are documented in the troubleshooting section.

library(JuliaCall)
julia <- julia_setup()
#> Julia version 1.7.2 at location /Applications/Julia-1.7.app/Contents/Resources/julia/bin will be used.
#> Loading setup script for JuliaCall...
#> Finish loading setup script for JuliaCall.

## If you want to use `Julia` at a specific location, you could do the following:
## julia_setup(JULIA_HOME = "the folder that contains Julia binary").
## You can also set JULIA_HOME in command line environment or use `options(...)`.

## Different ways of using Julia to calculate sqrt(2)

# julia$command("a = sqrt(2);"); julia$eval("a")
julia_command("a = sqrt(2);"); julia_eval("a")
#> [1] 1.414214
julia_eval("sqrt(2)")
#> [1] 1.414214
julia_call("sqrt", 2)
#> [1] 1.414214
julia_eval("sqrt")(2)
#> [1] 1.414214
julia_assign("x", sqrt(2)); julia_eval("x")
#> [1] 1.414214
julia_assign("rsqrt", sqrt); julia_call("rsqrt", 2)
#> [1] 1.414214
2 %>J% sqrt
#> [1] 1.414214

## You can use `julia$exists` as `exists` in R to test
## whether a function or name exists in Julia or not

julia_exists("sqrt")
#> [1] TRUE
julia_exists("c")
#> [1] FALSE

## Functions related to installing and using Julia packages

julia_install_package_if_needed("Optim")
julia_installed_package("Optim")
#> [1] "1.6.1"
julia_library("Optim")

Make sure the Julia installation is correct. JuliaCall can find Julia on PATH, and there are three ways for JuliaCall to find Julia not on PATH.

• Use julia_setup(JULIA_HOME = "the folder that contains julia binary")
• Use options(JULIA_HOME = "the folder that contains julia binary")
• Set JULIA_HOME in command line environment.

Such problems are usually on Linux machines. The cause for the problem is that R cannot find the libstdc++ version needed by Julia. To deal with the problem, users can export “TheFolderContainsJulia/lib/julia” to R_LD_LIBRARY_PATH.

The issue is usually caused by updates in R, and it can be typically solved by setting rebuild argument to TRUE in julia_setup() as follows.

JuliaCall::julia_setup(rebuild = TRUE)

This error happens when Julia is built/installed with MULTIARCH_INSTALL=1, as it is on e.g. Debian. It is caused by the bindir-locating code in jl_init not being multiarch-aware. To work around it, try setting JULIA_BINDIR=/usr/bin in .Renviron.

• One way to get help for Julia functions is just using julia$help as the following example:

julia_help("sqrt")
#> ```
#> sqrt(x)
#> ```
#> 
#> Return $\sqrt{x}$. Throws [`DomainError`](@ref) for negative [`Real`](@ref) arguments. Use complex negative arguments instead. The prefix operator `√` is equivalent to `sqrt`.
#> 
#> See also: [`hypot`](@ref).
#> 
#> # Examples
#> 
#> ```jldoctest; filter = r"Stacktrace:(\n \[[0-9]+\].*)*"
#> julia> sqrt(big(81))
#> 9.0
#> 
#> julia> sqrt(big(-81))
#> ERROR: DomainError with -81.0:
#> NaN result for non-NaN input.
#> Stacktrace:
#>  [1] sqrt(::BigFloat) at ./mpfr.jl:501
#> [...]
#> 
#> julia> sqrt(big(complex(-81)))
#> 0.0 + 9.0im
#> 
#> julia> .√(1:4)
#> 4-element Vector{Float64}:
#>  1.0
#>  1.4142135623730951
#>  1.7320508075688772
#>  2.0
#> ```
#> 
#> ```
#> sqrt(A::AbstractMatrix)
#> ```
#> 
#> If `A` has no negative real eigenvalues, compute the principal matrix square root of `A`, that is the unique matrix $X$ with eigenvalues having positive real part such that $X^2 = A$. Otherwise, a nonprincipal square root is returned.
#> 
#> If `A` is real-symmetric or Hermitian, its eigendecomposition ([`eigen`](@ref)) is used to compute the square root.   For such matrices, eigenvalues λ that appear to be slightly negative due to roundoff errors are treated as if they were zero More precisely, matrices with all eigenvalues `≥ -rtol*(max |λ|)` are treated as semidefinite (yielding a Hermitian square root), with negative eigenvalues taken to be zero. `rtol` is a keyword argument to `sqrt` (in the Hermitian/real-symmetric case only) that defaults to machine precision scaled by `size(A,1)`.
#> 
#> Otherwise, the square root is determined by means of the Björck-Hammarling method [^BH83], which computes the complex Schur form ([`schur`](@ref)) and then the complex square root of the triangular factor. If a real square root exists, then an extension of this method [^H87] that computes the real Schur form and then the real square root of the quasi-triangular factor is instead used.
#> 
#> [^BH83]: Åke Björck and Sven Hammarling, "A Schur method for the square root of a matrix", Linear Algebra and its Applications, 52-53, 1983, 127-140. [doi:10.1016/0024-3795(83)80010-X](https://doi.org/10.1016/0024-3795(83)80010-X)
#> 
#> [^H87]: Nicholas J. Higham, "Computing real square roots of a real matrix", Linear Algebra and its Applications, 88-89, 1987, 405-430. [doi:10.1016/0024-3795(87)90118-2](https://doi.org/10.1016/0024-3795(87)90118-2)
#> 
#> # Examples
#> 
#> ```jldoctest
#> julia> A = [4 0; 0 4]
#> 2×2 Matrix{Int64}:
#>  4  0
#>  0  4
#> 
#> julia> sqrt(A)
#> 2×2 Matrix{Float64}:
#>  2.0  0.0
#>  0.0  2.0
#> ```

• The GitHub Pages for this repository host the documentation for the development version of JuliaCall: https://non-contradiction.github.io/JuliaCall/.

• Also, you are more than welcome to contact me about JuliaCall at [email protected] or [email protected].

If you are interested in developing an R package which is an interface for a Julia package, JuliaCall is an ideal choice. You only need to find the Julia function or Julia module you want to have in R, using the module, and julia_call the function. There are some examples:

• diffeqr is a package for solving differential equations in R. It utilizes DifferentialEquations.jl for its core routines to give high performance solving of ordinary differential equations (ODEs), stochastic differential equations (SDEs), delay differential equations (DDEs), and differential-algebraic equations (DAEs) directly in R.
• convexjlr is an R package for Disciplined Convex Programming (DCP) by providing a high level wrapper for Julia package Convex.jl. convexjlr can solve linear programs, second order cone programs, semidefinite programs, exponential cone programs, mixed-integer linear programs, and some other DCP-compliant convex programs through Convex.jl.
• ipoptjlr provides an R interface to the Ipopt nonlinear optimization solver. It provides a simple high-level wrapper for Julia package [Ipopt.jl] (https://github.com/jump-dev/Ipopt.jl).
• FixedEffectjlr uses the Julia package FixedEffectModels.jl to estimate large fixed effects models in R.
• Julia MixedModels from R illustrates how to use JuliaCall and Julia package MixedModels.jl to build mixed models in R.
• autodiffr provides automatic differentiation to native R functions by wrapping Julia packages ForwardDiff.jl and ReverseDiff.jl through JuliaCall, which is a work in progress.

If you have any issues in developing an R package using JuliaCall, you may report it using the link: https://github.com/Non-Contradiction/JuliaCall/issues/new, or email me at [email protected] or [email protected].

JuliaCall is under active development now. Any suggestion or issue reporting is welcome! You may report it using the link: https://github.com/Non-Contradiction/JuliaCall/issues/new, or email me at [email protected] or [email protected]. You are welcome to use the issue template and the pull request template. The contributing guide provides some guidance for making contributions.

To check and test the JuliaCall package, you need to have the source package. You can

• download the source of JuliaCall from Github,
• open JuliaCall.Rproj in your RStudio or open R from the downloaded directory,
• run devtools::test() to see the result of the test suite.
• run devtools::check() or click the Check button in the RStudio Build panel in the upper right to see the result of R CMD check.

• RCall.jl is a Julia package which embeds R in Julia. JuliaCall is inspired by RCall.jl and depends on RCall.jl for many functionalities like type conversion between R and Julia.
• XRJulia is an R package based on John Chambers’ XR package and allows for structured integration of R with Julia. It connects to Julia and uses JSON to transfer data between Julia and R. A simple performance comparison between XRJulia and Julia can be found in JuliaCall JOSS paper.
• RJulia is an R package which embeds Julia in R as well as JuliaCall. It is not on CRAN yet, and I haven’t tested it.

JuliaCall is licensed under MIT.

Please note that the JuliaCall project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.

If you use JuliaCall in research that resulted in publications, then please cite the JuliaCall paper using the following BibTeX entry:

@Article{JuliaCall,
    author = {Changcheng Li},
    title = {{JuliaCall}: an {R} package for seamless integration between {R} and {Julia}},
    journal = {The Journal of Open Source Software},
    publisher = {The Open Journal},
    year = {2019},
    volume = {4},
    number = {35},
    pages = {1284},
    doi = {10.21105/joss.01284},
  }