A simple term rewriting system with Wolfram Language's syntax
Inspired by the book Write Yourself a Scheme in 48 Hours.
I decide to write myself a simple interpreter of Wolfram Language to learn more about Haskell as well as
achieve a deeper understanding about Mathematica, which is the desktop IDE for Wolfram Language.
ScreenShot
Running (Using Stack)
git clone https://github.com/jyh1/mmaclone.git
cd mmaclone/mmaclone
stack setup
stack build
stack exec mmaclone-exe
Prebulid binary files are available on the release page
Features
This interpreter is intended to mimic every exact detail of Wolfram Language, including but not limited to its syntax, semantic,
expression structure, evaluation details, etc. (All the scripts below were executed in the REPL session of the mmaclone program)
- The program support nearly all
Wolfram Language's syntax sugar, infix operators as well as their precedence. E.g., inequality expression chain is parsed to the same AST withWolfram Language.
In[1]:= FullForm[a==b>=c<=d<e]
Out[1]= Inequality[a,Equal,b,GreaterEqual,c,LessEqual,d]
Some more complicated examples.
In[2]:= FullForm[P@1@2//3]
Out[2]= 3[P[1[2]]]
In[3]:= FullForm[P''''[x]]
Out[3]= Derivative[4][P][x]
In[4]:= FullForm[Hold[(1 ##&)[2]]]
Out[4]= Hold[Function[Times[1,SlotSequence[1]]][2]]
Wolfram Language's powerful pattern matching is also implemented with scrupulous.
(*The famous bubble sort implementation*)
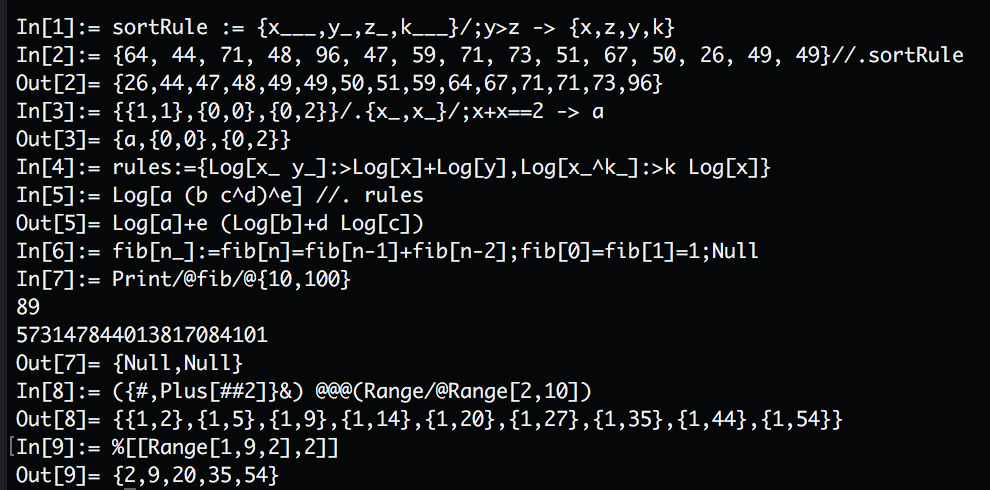
In[1]:= sortRule := {x___,y_,z_,k___}/;y>z -> {x,z,y,k}
In[2]:= {64, 44, 71, 48, 96, 47, 59, 71, 73, 51, 67, 50, 26, 49, 49}//.sortRule
Out[2]= {26,44,47,48,49,49,50,51,59,64,67,71,71,73,96}
(*Symbolic manipulation*)
In[3]:= rules:={Log[x_ y_]:>Log[x]+Log[y],Log[x_^k_]:>k Log[x]}
In[4]:= Log[a (b c^d)^e] //. rules
Out[4]= Log[a]+e (Log[b]+d Log[c])
Currently, the derivative function D is not built-in supported, but you could easily implement one with the powerful pattern matching facilities.
In[5]:= D[a_,x_]:=0
In[6]:= D[x_,x_]:=1
In[7]:= D[a_+b__,x_]:=D[a,x]+D[Plus[b],x]
In[8]:= D[a_ b__,x_]:=D[a,x] b+a D[Times[b],x]
In[9]:= D[a_^(b_), x_]:= a^b(D[b,x] Log[a]+D[a,x]/a b)
In[10]:= D[Log[a_], x_]:= D[a, x]/a
In[11]:= D[Sin[a_], x_]:= D[a,x] Cos[a]
In[12]:= D[Cos[a_], x_]:=-D[a,x] Sin[a]
(*performing derivative*)
In[13]:= D[Sin[x]/x,x]
Out[13]= -x^(-2) Sin[x]+Cos[x] x^(-1)
In[14]:= D[%,x]
Out[14]= -Cos[x] x^(-2)-(-2 x^(-3) Sin[x]+Cos[x] x^(-2))-x^(-1) Sin[x]
Pattern test facility is of the same semantic with `Wolfram Language`'s.
In[15]:= {{1,1},{0,0},{0,2}}/.{x_,x_}/;x+x==2 -> a
Out[15]= {a,{0,0},{0,2}}
In[16]:= {a, b, c, d, a, b, b, b} /. a | b -> x
Out[16]= {x,x,c,d,x,x,x,x}
In[17]:= g[a_*b__]:=g[a]+g[Times[b]]
In[18]:= g[x y z k l]
Out[18]= g[k]+g[l]+g[x]+g[y]+g[z]
In[19]:= q[i_,j_]:=q[i,j]=q[i-1,j]+q[i,j-1];q[i_,j_]/;i<0||j<0=0;q[0,0]=1;Null
In[20]:= q[5,5]
Out[20]= 252
- Some more interesting scripts
In[1]:= ((#+##&) @@#&) /@{{1,2},{2,2,2},{3,4}}
Out[1]= {4,8,10}
In[2]:= fib[n_]:=fib[n]=fib[n-1]+fib[n-2];fib[1]=fib[2]=1;Null
In[3]:= fib[100]
Out[3]= 354224848179261915075
In[4]:= fib[1000000000000]
Iteration Limit exceeded, try to increase $IterationLimit
In[5]:= Print/@fib/@{10,100}
55
354224848179261915075
Out[5]= {Null,Null}
More
For more information please refer to the project wiki (still under construction).
Features that are likely to be added in future versions:
(Some serious design errors are exposed during development, which I consider are inhibiting the project from scaling up. So currently my primary focus would be on refactor rather than adding new features/functions)
- More mathematical functions (
Sin,Cos,Modetc...) - Arbitrary precision floating arithmetic using GMP(GNU Multiple Precision Arithmetic Library), currently arbitrary integer, double and rational number are supported.
- More built-in functions (
Level,Import,Derivativeetc...) - More sophisticated pattern matching
head specification (of the form Blank[Head], currently it only support list type)(Implemented)Pattern Test(Implemented)BlankSequence, BlankNullSequence(Implemented)- Other pattern matching expression, like
Verbatim,Longest
RecursionLimit(Implemented)- Negative index e.g. in
Part - Negative level specification
- Curried function e.g.
f[a][b](currently it will throw an error if one is trying to attach value to the curried form throughSetorSetDelayed) - Use iPython as front end
Replace String implementation with more efficient Text(Implemented)